メルカトルの呪い？地図のおはなし

今回はNonrealさんのブログ『海国防衛ジャーナル』からご寄稿いただきました。
※すべての画像が表示されない場合は、https://getnews.jp/archives/296931をごらんください。

メルカトルの呪い？地図のおはなし

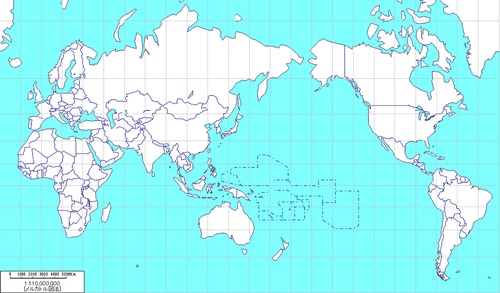
突然ですが、平面の世界地図を想像してみて下さい。

人によって違うと思いますが、「中国や北朝鮮から日本を越えて右にず～っとまっすぐ行くと北米大陸がある」という図1のような地図を想像する方が多いのではないでしょうか。

（図1）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu011.jpg

この地図は正角円筒図法というもので、メルカトル図法として知られています。単に世界地図を想像しろと言われてこの地図が浮かんでくること自体は何ら問題ではありません。

しかし、「平壌を中心にロサンゼルスまでの弾道ミサイルの飛翔経路」について議論する場合、メルカトル図法は不適切です。メルカトル図法でみると、平壌からロサンゼルスに向けて発射された弾道ミサイルは日本の上空を通るように思われますが、実際はそうではありません（後述、参照記事 *1）。

*1:「北朝鮮・中国→米本土の弾道ミサイルは日本上空を通過しません」 2012年04月07日 『海国防衛ジャーナル』
http://blog.livedoor.jp/nonreal-pompandcircumstance/archives/50660403.html

この点、誤解されている方が少なくないようです。メルカトル図法がとてもポピュラーで見慣れたものであることの弊害かもしれませんね。さすがに専門家の方はそのような誤りをすることはありませんが、新聞やテレビなどの議論では時々「あれ？」という場面があります。個人的にはこれを「メルカトルの呪い」と呼んでいます(；一_一)

弾道ミサイルやミサイル防衛（MD）に関する話をする上で、メルカトル図法思考がもたらす問題とは？　どのような地図を頭に描けば良いのか？　本稿では、こうした地図に関するはじめの一歩のそのまた一部分をまとめてみます。

全ての情報が正しい平面地図はない

地図は、球体の情報をむりやり平面に表現したものです。したがって、平面に投影された地図は、距離、角度、面積のどこかに必ずひずみがあり、どのような図法を用いても3つのひずみ全てを同時に解消することはできません。使用目的に応じた地図を選択することが大切になりますね。

地図をおおざっぱに分類すると以下のようになります。

【性質で分類】

正距図法：距離が正しい。
正積図法：面積が正しい。
正角図法：任意の二地点間を結んだ直線と経線のなす角度が正しい。

【投影法で分類】

方位図法：地球の周辺に置かれた平面に地球の姿を投影する。
円錐図法：地球に傘のような円錐をかぶせて地球の姿を投影し、平面に切り広げる。
円筒図法：地球に帯を巻くように円筒をかぶせて地球の姿を投影し、平面に切り広げる。

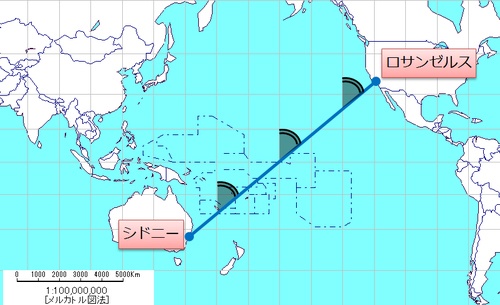
メルカトル図法は、先述の通り正角円筒図法です（地球は丸いので、緯線の長さは赤道が最大で極に近づくにしたがって短くなりますが、メルカトル図法では全ての緯線を赤道と同じ長さに拡大します。経線もそれぞれの緯線の拡大率に応じて拡大します（図1参照）。経緯線の拡大率が等しくなるので、それらがなす角度も等しくなります）。「任意の二地点間を結んだ直線と経線のなす角度が正しい」わけですが、正距図法や正積図法に比べて何が正しいのかいまひとつ分かりませんよね？　文字にすると小難しいので、図解してみます（図2）。シドニー～ロサンゼルスの二地点間を例にとってみましょう。

（図2）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu02.jpg

シドニー～ロサンゼルスの間を結んだ直線と経線のなす角度を黒く塗りつぶしてあります。メルカトル図法が正しいのは、ここの角度です。

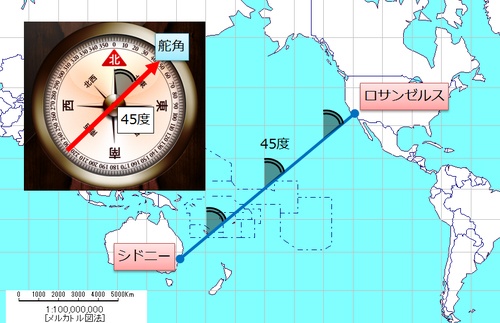
メルカトル図法の適切な利用法は航海図です。シドニー～ロサンゼルス間の場合、東方向にだいたい45度で経線と交わっているので、実際に船の舵を取るときには、航路の角度（舵角）を北に対して45度に保って東へ向かえば、いずれ目的地に到着することになります（図3）。

（図3）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu03.jpg

メルカトル図法がまねく錯覚

メルカトル図法は「任意の二地点間を結んだ直線と経線のなす角度」の正しさを保つために、面積や方位・距離の正しさを犠牲にしています。ところが、地図といえばメルカトル！というほどに見慣れた地図であることから、面積や方位を話題にした場合でもメルカトル図法の地図が用いられてしまうことがあります。これが、メルカトルの呪いと呼ばれる（呼ばれてない）悲劇の始まりです。

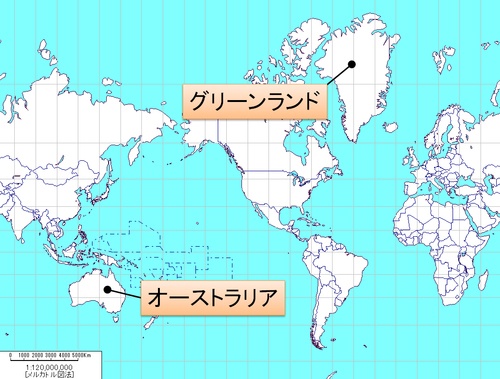
例えば、グリーンランドとオーストラリアの面積を見比べてみましょう。

まずはメルカトル図法で。

（図4）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu04.jpg

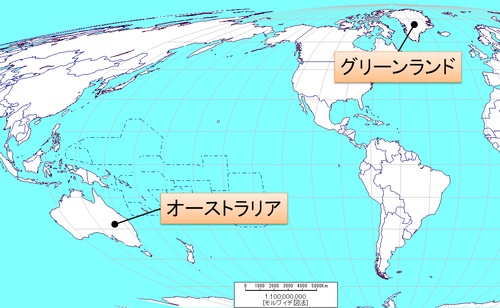
圧倒的にグリーンランドが広いですね。次に、面積を正しく表した正積図法（モルワイデ図法）で見ると…

（図5）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu05.jpg

今度はオーストラリアの方が広く見えます。実際の面積を数字で見ると、グリーンランド（2,166,086平方km）、オーストラリア（7,692,024平方km）ですから、オーストラリアが3倍以上も大きいのです。メルカトル図法は緯度が高くなるにしたがって面積や距離が拡大されるので、北極に近いグリーンランドは実際よりもはるかに大きく表示されてしまうわけです。

もしメルカトル図法を面積の議論で用いれば、とんでもない間違いが起きてしまうかもしれません。

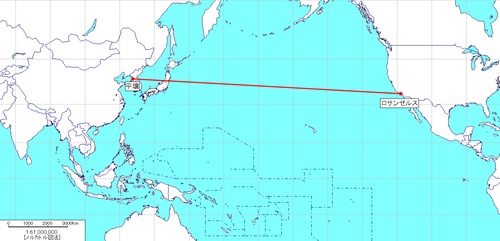
次に、本稿の主旨である方位と距離に注目してみましょう。北朝鮮の平壌からロサンゼルスに向かう弾道ミサイルの軌道をメルカトル図法上に描いてみます。

（図6 メルカトル図法で平壌→ロサンゼルス）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu06.jpg

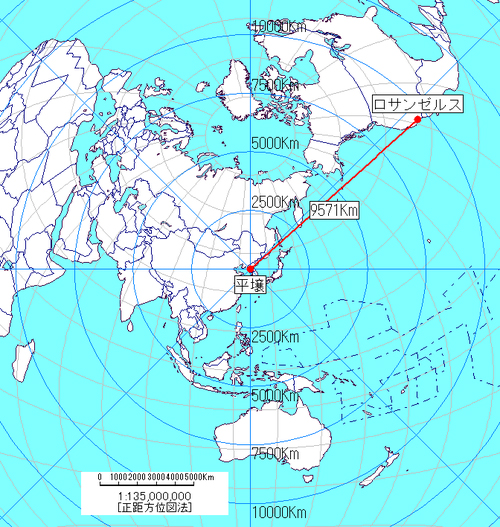
むむ、ミサイルが日本の上空を通過しますね。けしからんことです。でも、メルカトル図法は方位を正しく教えてくれるものではありません。ここはいったん落ち着いて、距離と方位を正しく示す正距方位図法を用いてみましょう。

（図7 正距方位図法で平壌→ロサンゼルス）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu07.jpg

日本の上空を通過しませんね。

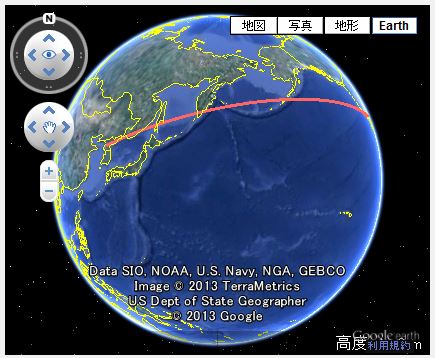
念のために、グーグルアースで立体的に確認しておきます。

（図8 グーグルアースで平壌→ロサンゼルス）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu08.jpg
（※実際のページで見る場合は、グーグルアースのPlug-inのインストールが必要です）
（※図8のグーグルアースが、safariだと通常のグーグルマップとして表示されるようです(T_T)）

正距方位図法と同じ軌跡ですね。日本の上空は通過しません（地球の自転によるコリオリの力を加味しても日本を通過しないのは同じ。）。

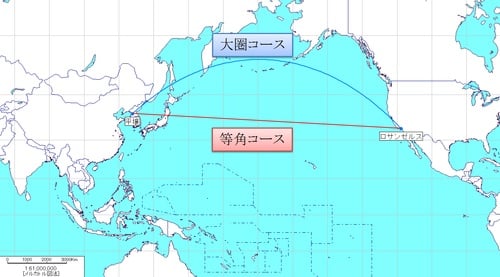
このように、メルカトル図法で二地点間を結んだコース（等角コース）は、実際の地球上の二地点間の最短コース（大圏コース）ではないのです。

（図9 平壌→ロサンゼルスの等角コースと大圏コース。メルカトル図法）

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/chizu09.jpg

弾道ミサイルは巡航ミサイルと違い、大きくS字を描くような飛翔をすることはありません。1万kmほども飛翔するICBMともなるとできるだけ無駄な燃料を搭載したくないですから、目的地までの最短距離＝大圏コースをたどります。

◇　◇　◇

北朝鮮や中国の思考がどれほど常軌を逸したものであったとしても物理法則には逆らえませんし、地球が丸い事実も私たちと共有するしかありません。現時点で、米本土を狙った弾道ミサイルが日本の上空を通過することはないでしょう。このことは、メルカトル図法では理解できません。

しかし、彼らの弾道ミサイルは我が国の安全保障にとって間違いなく脅威です。その脅威を正しく知り、正しく備えるためにも、適切な地図の上で考えたいものですね。

執筆：この記事はNonrealさんのブログ『海国防衛ジャーナル』からご寄稿いただきました。

寄稿いただいた記事は2013年03月08日時点のものです。