折り紙準結晶

今回は佐藤健太郎さんのブログ『有機化学美術館・分館』からご寄稿いただきました。

折り紙準結晶

古くからの読者の方はご存知の通り、筆者の趣味は折り紙です。この趣味の人間は、形あるものなら何でも紙で折ってみようとするものです。で、筆者もふと思いつきました。今年ノーベル賞を受賞した、準結晶をなんとか折り紙で作れないものか。

「第3の固体・準結晶の発見にノーベル化学賞」 2011年10月06日 『有機化学美術館・分館』
http://blog.livedoor.jp/route408/archives/51952099.html

この図形（トップ画像参照）、角度が36°・144°のひし形と、72°・108°のひし形から成ります。このパーツをひとつひとつ折り紙で作って組んでいけばいいわけですが、実は辺の長さをそろえようとすると結構面倒であることに気づきました。三角関数とかを駆使して計算し、面倒くさい紙の切り出しをする必要があります。うーむ、どうすっかな……（-_-）。

と、筆者はここでひらめきました！　筒状の角柱を作り、これを上から見れば簡単にサイズのそろったひし形が作れるではないか！　これなら面倒な計算なしに、サイズ合わせが可能ですよ！　（べっ、別に三角関数の計算ができないわけじゃないんだからねっ！　より簡便な技法をみなさんに提供したいだけなんだからねっ！）

こういうことっすね。

用紙は折り紙や紙テープを切ってもいいし、なんならチラシの裏でも何でもいいわけですが、ここでもうひとつひらめきました！　ポストイット、和風にいえば付箋を使えばよいではないか！　ついているのりも役立ちます。

ポストイット『ふせんハーフ』

付箋用紙はわざわざ切るまでもなく細長いものが売っていますし、カラフルで紙質のいいものがたくさん手に入るので、気兼ねなく使えるのもいいところです。筆者は手元にあったポストイットふせんハーフを使いましたが、100円ショップのものでも十分でしょう。この規格は12.5mm×75mm、つまり1:6の比率です。

こんな感じで6等分してゆく。

で、これを一番上の写真のように四角柱の形に巻き、外側を付箋ののりで止めれば完成。図解するとこういう感じです。

上から見たところ。巻くように折って止める。

うむ、賢いな俺！　ふだんの仕事でもこれくらい頭が回ればいいんだがな！　まあとにかくこの要領でガシガシと作っていきます。ひし形は36°と72°の2種類ですから、これを水色とピンクで色分けして作ってみます。

量産ッ！

さらに量産ッ！　折り出したら止まらない、折り紙界の暴走特急とは俺のことだッ！
（↑落ち着け馬鹿）

で、これを側面にのりをつけてぺたぺた貼り合わせてゆきます。

まず正10角形。

注意すべきは、5回転対称を保ちながら貼っていくこと。またひし形の角度は先ほども述べたように36°を基本としています。36°を1単位としたとき、2 種のひし形の頂点はそれぞれ1,4と2,3になります。ですので1点に10単位、すなわち360°が集まるように貼っていけば間違いありません。

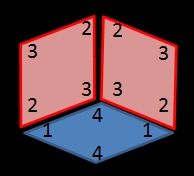
1頂点に10単位が集まるよう貼り合わせる。

貼っていくッ！

まあこのへんにしといたるわ！

実はこの形、上記のルールさえ守っていれば、どう貼ろうと破綻せずにどこまでも広げていけます。かなり柔軟性の高い形であることが実感でき、このへんは実際に作ってみて初めてよくわかるところです。材料も手近で手に入りますし、科学教室のワークショップの題材などにいかがでしょうか。

ただこれは実は準結晶ではなく、その2次元版というべきペンローズタイルですから、“折り紙準結晶”というのは若干誇大広告です。3次元版も現在考えておりますので、できたらまた発表いたします。

ということでまた！

※角柱を木口から見るというアイディアは、川崎敏和氏の『バラと折り紙と数学と』から拝借しました。

執筆： この記事は佐藤健太郎さんのブログ『有機化学美術館・分館』からご寄稿いただきました。