データ分析の不思議、シンプソンのパラドックスを統計的因果推論から考える（Unboundedly）

2018/09/02 13:00 寄稿

今回はKRSKさんのブログ『Unboundedly』からご寄稿いただきました。

データ分析の不思議、シンプソンのパラドックスを統計的因果推論から考える（Unboundedly）

今回は統計学で有名な「シンプソンのパラドックス」という問題について紹介したいと思います。簡単にいえば、同じデータでも分析の仕方によって全く矛盾したように見える結果が得られるというお話です。データだけ見ると、信じがたいような直感に反する現象がおきるので頭の体操としてとても面白いです。

あまりに有名なパラドックスであるため日本語でも解説がいくつか出ていますが、人によって言っていることが違っていたり、不完全であったりします。多くはシンプソンによるオリジナルの論文を読んでないことから起因するのだと思います。

例えばシンプソンのパラドックスを交絡*1 の問題だと捉える人は多いですが、個人的に不完全だと思います（間違いではない）。このように誤解が広まった歴史的背景も含めて、詳しく書いていきたいと思います。ちなみにアニメのシンプソンズはこの問題と全く無関係です。

*1：「#ニセの関連が生じるパターン１：交絡 (【点と矢印で因果関係を考える】データからニセモノの関連が生じるパターンとその対策まとめ：因果ダイアグラム（DAG）によるバイアスの視覚的整理)」2017年03月22日『Unboundedly』
https://www.krsk-phs.com/entry/structural_bias#%E3%83%8B%E3%82%BB%E3%81%AE%E9%96%A2%E9%80%A3%E3%81%8C%E7%94%9F%E3%81%98%E3%82%8B%E3%83%91%E3%82%BF%E3%83%BC%E3%83%B3%EF%BC%91%E4%BA%A4%E7%B5%A1

目次
1. そもそもシンプソンのパラドックスとは？
2.シンプソンのパラドックスの歴史的背景
3.関連の逆転はなぜ”パラドックス”なのか
4.パラドックスは「交絡」の問題？
5.Simpsonが本当に伝えていたのは・・・
6.関連資料

そもそもシンプソンのパラドックスとは？

シンプソンのパラドックスを説明する際によく使われる例が次のようなものです。

ある病気を予防する効果が期待される新薬Aが開発され、従来の治療法（コントロール群）と効果の違いを比較したいとしましょう。ランダム化比較試験*2 ができると一番いいのですが、ここでは次の表にある観察データしか手に入らなかったとします。

*2：「#ランダム化という魔法（データから因果関係をどう導く？：統計的因果推論の基本、「反事実モデル」をゼロから）」2018年08月05日『Unboundedly』
https://www.krsk-phs.com/entry/counterfactual_assumptions#%E3%83%A9%E3%83%B3%E3%83%80%E3%83%A0%E5%8C%96%E3%81%A8%E3%81%84%E3%81%86%E9%AD%94%E6%B3%95

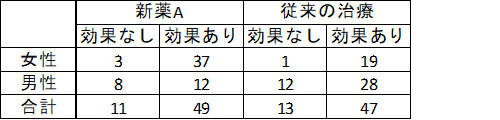
まず女性だけに注目して、新薬Aと従来の治療を比較してみます。治療の効果があった人の割合は、

新薬A → 37/(3+37) = 37/40 = 0.925

従来の治療 → 19/(1+19) = 19/20 = 0.95

つまり新薬Aを飲んだ人の92.5％に効果があったのに対して、従来の治療を受けた人では95％に効果があったということです。直感的に、「女性では従来の治療のほうが良さそう」と思わせるデータです。

つぎに男性だけに注目して、同じような比較を行います。

新薬A → 12/(8+12) = 12/20 = 0.6

従来の治療 → 28/(12+28) = 28/40 = 0.7

新薬Aを飲んだ人の60％に効果があったのに対して、従来の治療を受けた人では70％に効果があったということです。やはり、「男性においても従来の治療のほうが良さそう」と思わせるデータです。

では一番下の行、男女合わせたデータを見てみましょう。

新薬A → 49/(11+49) = 49/60 ≒ 0.82

従来の治療 → 47/(13+47) = 47/60 ≒ 0.78

男女合わせた集団全体でみると、新薬Aを飲んだ人の82％に効果があったのに対して、従来の治療を受けた人では78％にしか効果がありません。つまり、「従来の治療より新薬Aのほうが効果が良さそう」と思わせるデータです。

さて、ここで一つの疑問が出ると思います。

男性でも女性でも効かないが、”人間”（男女合計）には効果が高い新薬Aなるものが存在しうるのでしょうか？※1

男性でも女性で効かないなら、男女関係なく効かないので集団全体で見ても効果がないと考えるのが自然な発想です。このように、集団全体を見た時とその小集団に注目した時で一見矛盾したような結論がデータから導かれてしまうことを指して、「シンプソンのパラドックス」と呼びます。

シンプソンのパラドックスの歴史的背景

シンプソンのパラドックスを知るうえで重要な論文が二つあります。

一つ目はパラドクスの名前にあるSimpsonが1951年に発表した論文。

Simpson, Edward H. “The interpretation of interaction in contingency tables.” Journal of the Royal Statistical Society. Series B (Methodological) (1951): 238-241.

二つ目は、Blythが1972年に発表した論文。Simpson(1951）に書かれた現象を「シンプソンのパラドックス」と名づけ、解説を試みています。

Blyth, Colin R. “On Simpson’s paradox and the sure-thing principle.” Journal of the American Statistical Association 67.338 (1972): 364-366.

一般的にはBlythによって解説された内容、およびBlyth(1972)で使われている例がシンプソンのパラドックスを説明するときに使われています。上記の新薬Aの例も、（細かい違いはありますが）Blythや彼の論文を参考にパラドックスを理解しようとしたPearl*3 が使ったものです。

*3：「#参考資料 (【点と矢印で因果関係を考える】データからニセモノの関連が生じるパターンとその対策まとめ：因果ダイアグラム（DAG）によるバイアスの視覚的整理)」2017年03月22日『Unboundedly』
https://www.krsk-phs.com/entry/structural_bias#%E5%8F%82%E8%80%83%E8%B3%87%E6%96%99

「シンプソンのパラドックス」という言葉の名づけ親なので、その説明にBlyth(1972)を参照するのは自然なのですが、BlythはSimpsonの言っていることを完全に理解しているとはいいがたいのです。そのため、不完全な理解が広がってしまっているのだと思います。

実はSimpson(1951)から得られる教訓はBlyth(1972)が主張している以上のものだと考えられます。

パラドックスは「交絡」の問題？

前述のBlythやPearlらは、シンプソンのパラドックスは本質的に交絡の問題だと捉えています。

交絡はDAGを使うことで、視覚的に理解することができます。つまり因果関係を注目している二つの要因（例：新薬Aと病気Yへの効果）の共通原因Cが存在する場合は、そのCを条件付けしなければ得られる関連が因果関係を意味しないというものです。DAGに基づく交絡の定義についてはこちらをどうぞ。*4

*4：「#ニセの関連が生じるパターン１：交絡 (【点と矢印で因果関係を考える】データからニセモノの関連が生じるパターンとその対策まとめ：因果ダイアグラム（DAG）によるバイアスの視覚的整理)」2017年03月22日『Unboundedly』
https://www.krsk-phs.com/entry/structural_bias#%E3%83%8B%E3%82%BB%E3%81%AE%E9%96%A2%E9%80%A3%E3%81%8C%E7%94%9F%E3%81%98%E3%82%8B%E3%83%91%E3%82%BF%E3%83%BC%E3%83%B3%EF%BC%91%E4%BA%A4%E7%B5%A1

上記の例の場合、もしかすると性別によってどちらの治療を好むかが異なるかもしれません。また、性別によって病気のリスクも異なるかもしれません。例えば次のようなDAGが成立する可能性があります。

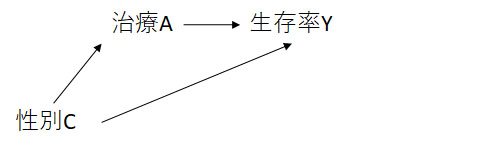
この場合、Cを条件づける必要があります。条件づけにはいろいろな方法がありますが、最もシンプルなのはCの値が同じ集団でAとYの関連を見るというアプローチです。つまり、男女別で関連を見るというのは性別を条件づけるのと同じと理解できます。回帰分析を使って”調整”するのも同じ考え方です。

このような第三因子Cを条件づけすべきかどうかは、データから判断できるものではなく、性別と治療・病気リスクの関係性を（その他の研究や、臨床現場の実態などを参考に）自分の頭で考え、DAGに表現する必要があります。

AとYの両方と関連している要因Cが交絡であると考える人もいます。実際に上の表にあるデータを使って計算すると、女性のほうが新薬で治療されている割合が高く、病気を発症する割合が高いことがわかります。しかし、このような統計的な基準を用いて交絡因子かどうかを判断するのは危険です。この記事の例４*5 で示しているような状況下では、AとYに関連するCを条件づけることでかえってバイアスをもたらしてしまいます。

*5：「#ニセの関連が生じるパターン１：交絡 (【点と矢印で因果関係を考える】データからニセモノの関連が生じるパターンとその対策まとめ：因果ダイアグラム（DAG）によるバイアスの視覚的整理)」2017年03月22日『Unboundedly』
https://www.krsk-phs.com/entry/structural_bias#%E3%83%8B%E3%82%BB%E3%81%AE%E9%96%A2%E9%80%A3%E3%81%8C%E7%94%9F%E3%81%98%E3%82%8B%E3%83%91%E3%82%BF%E3%83%BC%E3%83%B3%EF%BC%91%E4%BA%A4%E7%B5%A1

非常に重要なので繰り返しますが、あくまで自分の頭を使って、注目している要因間の関係性（DAG)を考えたうえで、第三の要因Cを条件づけるべきかどうかを考える必要があります。

よって、上記のDAGが正しいと仮定してパラドックスを交絡の問題として捉えると、性別で条件すべきであり、男女別でみた関連から得られる「従来の治療のほうが効果が高い」という結論のほうが正しそうだと考えることができます。

Simpsonが本当に伝えていたのは・・・

実はシンプソンのパラドックス（データを合計するのか、分けて分析するのかで関連が変わること）を交絡の問題と一括りにするのは早計だといえます。

それどころか、Simpsonが1951年に発表した論文では関連の方向性が”逆転”する例はでてきません。彼が1951年の論文の中で使った例は以下のようなもの。

トランプのカードが合計52枚あるとします（ジョーカー抜き）。トランプには赤色（ハートとダイヤ）と黒色（スペードとクローバー）が半々、26枚ずつあります。また絵柄（J, Q, K)は赤黒6枚ずつ、合計12枚あります。一度でもトランプで遊んだことがある人にとっては当たり前の事実です。

これをデータとして表に示すと、

当然ですが、カードの色と柄カードの割合に関連はありません。柄カードも数字カードも半分ずつ赤色カードと黒色カードを含んでいます。

Simpsonはさらに、「赤ちゃんがトランプで遊んでいていくつかのカードが汚れている」という状況を考えました。

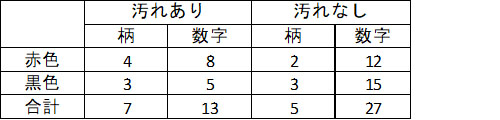
この時、「汚れあり」「汚れなし」のカード別々に注目すると、それぞれ「柄カードより数字カードのほうが赤色が多い」といえます。では、「柄によってカードの色の割合が異なるようにトランプが作られている」と考えていいのでしょうか？”直感的に“違うとわかります。汚れの有無別ではなく、カード全体で割合を比較するほうが正しいということです。

Simpsonはさらに次のような例を出しました。ある治療をうけたか受けないかで、患者が生きることができたかできなかったか、その結果を男女別に示しています。その治療は、患者の生存に非常に影響する重要なものであると期待されているものであると仮定します。

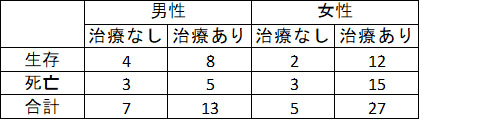
男性でみても女性でみても、治療ありのほうが生存率が高いです（例：男性だと4/7 < 8/13）。治療の効果あり！と考えたいところですが、ここでよくよくデータを見てみると実はこれ先ほどのトランプの例と全く同じ表なのです。トランプの色と柄が、それぞれ生存と治療の有無に対応しています。つまり、男女を合計した集団全体で見ると、「治療と生存率に関連なし」という結果になってしまうのです。なんとなく”直感的に”男女別の結果のほうが正しいような気がするのですが、根拠はありません。

Simpsonの出した例は、「全く同じデータでも、”もっともらしい解釈”ができる分析方法はシナリオによって異なる」ことを伝えています。この、”もっともらしい解釈”をSimpsonはsensible interpretationと呼んでいます。トランプの例ではグループ分けしないほうがいいし、治療の例では男女別したほうがよさそうです。

Simpson自体は、Sensible Interpretationは直感に基づいて判断するものだとしています。この論文が書かれた時代はまだ交絡だとか、因果推論に関する考え方が広まっていない時代なので仕方がありません。

しかし、統計的因果推論に対する考え方が深まった現代、このオリジナル版シンプソンのパラドックスは直感ではなくDAGのルールにのっとり、条件付けをすべきかどうか判断できます。

DAGルールは以下の記事をどうぞ。

トランプの例では、赤ちゃんが数字カードよりも柄カードを好んで遊んでいた、黒色カードよりも赤色カードを好んで遊んでいたと考えられます。この場合の対応するDAGは、

汚れは、カードの柄・色によって決められる共通効果（Collider)として考えられます。この場合、Cを条件づけると選択バイアス*6 を引き起こしてAとYの間に因果関係が存在しなくても（A→Yの矢印がないことに注意）関連が生じることになります。

*6：「#ニセの関連が生じるパターン２：選択バイアス (【点と矢印で因果関係を考える】データからニセモノの関連が生じるパターンとその対策まとめ：因果ダイアグラム（DAG）によるバイアスの視覚的整理)」2017年03月22日『Unboundedly』
https://www.krsk-phs.com/entry/structural_bias#%E3%83%8B%E3%82%BB%E3%81%AE%E9%96%A2%E9%80%A3%E3%81%8C%E7%94%9F%E3%81%98%E3%82%8B%E3%83%91%E3%82%BF%E3%83%BC%E3%83%B3%EF%BC%92%E9%81%B8%E6%8A%9E%E3%83%90%E3%82%A4%E3%82%A2%E3%82%B9

逆に治療の例では、男性のほうが(面倒くさがるなどして）治療を受けにくく、しかし一般的に男性のほうが生存率が高いとしましょう。この場合のDAGは、

性別が治療の選択や生存率に影響する、共通原因（Common cause)として機能しています。このような状況では、男女合わせた分析（Cを条件付けない）は性別による交絡バイアスをもたらします。男女別の解析が必要になります。

ここで重要なのは、

①全く同じデータでも、Cが共通効果なのか共通原因で必要な分析方法が全く異なるということ

②Cが共通効果なのか共通原因なのかは、データ単独では判断できない。注目している要因間の関係性を考える（DAGを書く）必要あり。

つまり言い換えると、

データから得られる関連に因果的な解釈をしたい場合、どのような分析が適切かをデータドリブンで決めることはできない。

ということです。したがってシンプソンのパラドックスは単なる交絡の問題というよりは、統計的因果推論の根本的な難しさを教えてくれる良い例だと思います。

これらの考え方は、ハーバード大のMiguel Hernan教授が書いた以下の論文と以下のHernan氏のツイートにも綺麗にまとまってあります。

Hernán, Miguel A., David Clayton, and Niels Keiding. “The Simpson’s paradox unraveled.” International journal of epidemiology 40.3 (2011): 780-785.

I thought I understood Simpson's paradox until I read Simpson’s paper. Turn out to be more interesting than expected https://t.co/FemiUsb9X2 pic.twitter.com/iEOcwR3fwa

— Miguel Hernán (@_MiguelHernan) 2017年5月5日

I thought I understood Simpson’s paradox until I read Simpson’s paper. Turn out to be more interesting than expected http://bit.ly/2noUXcG

機械学習・AI研究ブームですが、コンピューターにデータを与えてぽちっとやれば因果関係がわかるという世界は（少なくとも現時点では）非現実的です。