統計的消去で擬似相関を見抜こう！

今回はhoxo_mさんのブログ『ほくそ笑む』からご寄稿いただきました。
※すべての画像が表示されない場合は、https://getnews.jp/archives/381597をごらんください。

統計的消去で擬似相関を見抜こう！

今日は初心者向け記事です。

はじめに

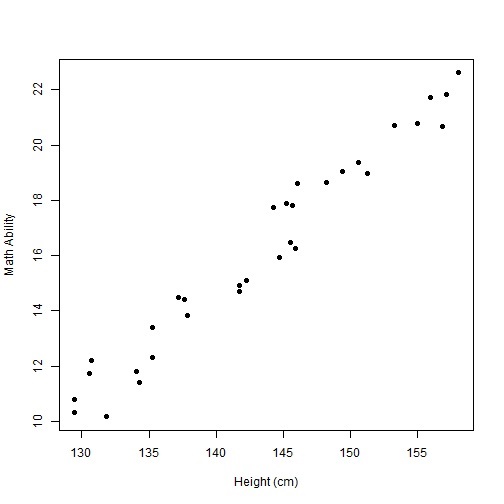
ある範囲の年齢の小学生32人を無作為に選び、算数のテストを受けてもらい、さらにその身長を測定しました。

身長に対する算数の点数のグラフは次のようになりました。

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/24.jpg

なんと、身長の高い子供の方が、算数の点数が高いという結果になりました！

身長が算数の能力に関係しているなんて、すごい発見です！

しかしながら、結論から言うと、この結果は間違っています。

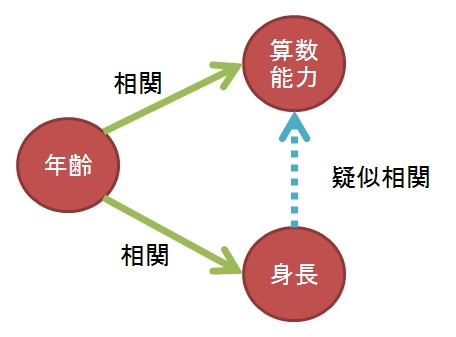
なぜなら、抽出したのは「ある範囲の年齢の小学生」であり、年齢の高い子も低い子も含まれているからです。

年齢が高いほど算数能力は高くなり、年齢が高いほど身長も高くなることは容易に推測できます。

この関係を図で表すと次のようになります。

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/32.jpg

つまり、年齢と算数能力に相関があり、年齢と身長にも相関があるため、身長と算数能力にも見かけ上の相関が見えているのです。

このような相関を擬似相関と言います。

統計解析では、このような擬似相関に騙されてしまうと、誤った結論を導いてしまいます。

今日は、擬似相関に騙されないために、疑似相関を見抜く統計的テクニックについて説明しようと思います。

データの準備

まずはデータの準備です。

データとしては上で説明したものを使用します。

data <- read.table("http://dl.dropboxusercontent.com/u/432512/20130708/SchoolChildrensMaths.txt", header = TRUE) head(data)

## AMA YEARS HGT
## 1 10.31 5.0 129.4
## 2 10.77 5.2 129.5
## 3 10.16 5.4 131.8
## 4 11.73 5.6 130.5
## 5 12.20 5.8 130.7
## 6 11.40 6.0 134.3

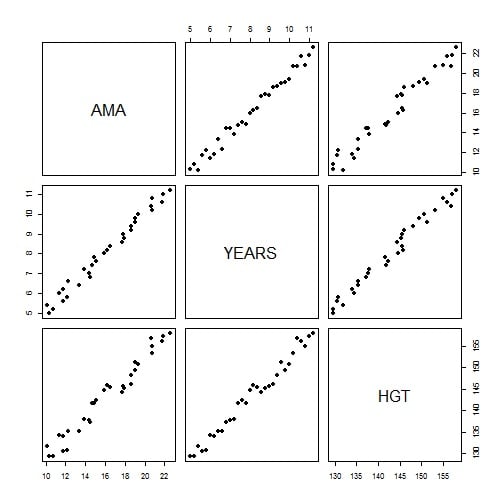
算数の平均点数(AMA)、年齢(YEARS)、身長(HGT)が入ったデータです。

プロットしてみると、すべての変数間に相関が見られます。

pairs(data, pch = 19)

(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/42.jpg

このようなデータから、どのようにして疑似相関を見抜けばよいでしょうか？

擬似相関を見抜くには

擬似相関を見抜くには、統計的消去(statistical elimination)を行います。

統計的消去とは、解析結果からある変数の影響を取り除くことです。

具体的に見ていきましょう。

今、身長と算数能力の関係を見たいとします。

ただし、これらの変数は年齢に影響されますので、年齢の影響を取り除いて、純粋な2変数間だけの関係を見たいのです。

ここで、次のように考えてみます。

もし、年齢に対する標準身長というものがわかれば、身長から標準身長を引いたもの(残差)というのは、年齢に影響されない身長データと見なすことができるのではないでしょうか。

これは算数能力についても言えるので、そうやって計算された2つの残差間の関係を見れば、年齢の影響を取り除いた上で解析をしているのと同じことになります。

そこで、まずは年齢に対する標準身長を回帰分析で求めてみます。

par(mfrow = c(1, 2))
model1 <- lm(HGT ~ YEARS, data) plot(HGT ~ YEARS, data, xlab = "Years", ylab = "Height", pch = 19) abline(model1) resid1 <- residuals(model1) plot(resid1 ~ YEARS, data, xlab = "Years", ylab = "Height(Residuals)", pch = 19) abline(h = 0)

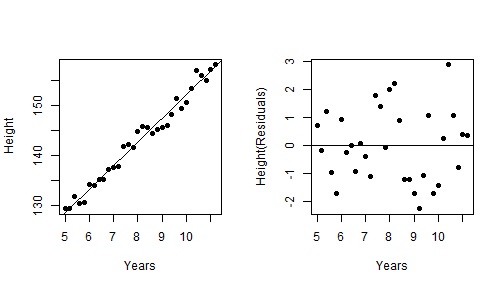
(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/51.jpg

左図は回帰直線、右図は残差です。

右図は左図の回帰直線を水平になるまで回転させたものだと思ってください。

これが年齢の影響を取り除いた身長データになります。

同様にして、年齢に対する標準的な算数能力について求め、年齢の影響を取り除いた算数能力データを作成します。

par(mfrow = c(1, 2))
model2 <- lm(AMA ~ YEARS, data) plot(AMA ~ YEARS, data, xlab = "Years", ylab = "Math Ability", pch = 19) abline(model2) resid2 <- residuals(model2) plot(resid2 ~ YEARS, data, xlab = "Years", ylab = "Math Ability(Residuals)", pch = 19) abline(h = 0)

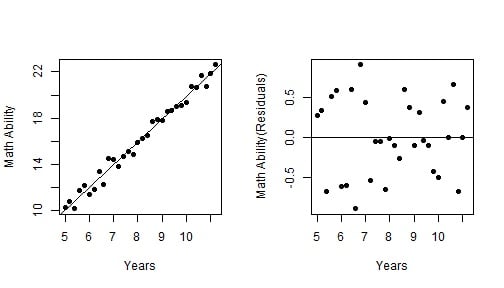
(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/6.jpg

もし、身長と算数能力が真の相関関係にあるならば、これらの残差(年齢の影響を取り除いたデータ)の間に相関が見られるはずです。

model3 <- lm(resid2 ~ resid1) plot(resid2 ~ resid1, xlab = "Height(Residuals)", ylab = "Math Ability(Residuals)", pch = 19) abline(model3)

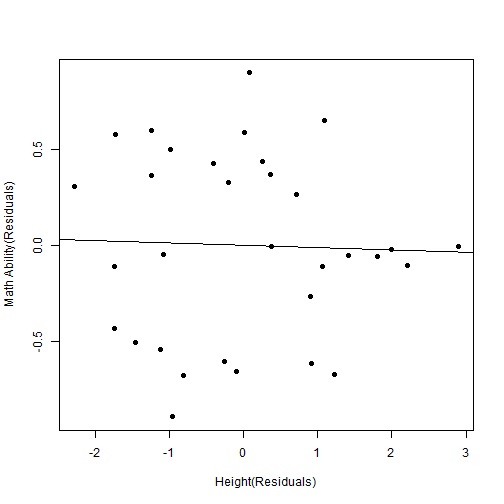
(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/7.jpg

どうやら、これらの値には相関は見られないようです。

したがって、身長と算数能力との関係が擬似相関であったことが分かります。

さて、同様にして、年齢と算数能力との関係から、身長の影響を取り除いてみましょう。

par(mfrow = c(2, 2))
model4 <- lm(YEARS ~ HGT, data) plot(YEARS ~ HGT, data, xlab = "Height", ylab = "Years", pch = 19) abline(model4) resid4 <- residuals(model4) plot(resid4 ~ HGT, data, xlab = "Height", ylab = "Years(Residuals)", pch = 19) abline(h = 0) model5 <- lm(AMA ~ HGT, data) plot(AMA ~ HGT, data, xlab = "Height", ylab = "Math Ability", pch = 19) abline(model5) resid5 <- residuals(model5) plot(resid5 ~ HGT, data, xlab = "Height", ylab = "Math Ability(Residuals)", pch = 19) abline(h = 0)

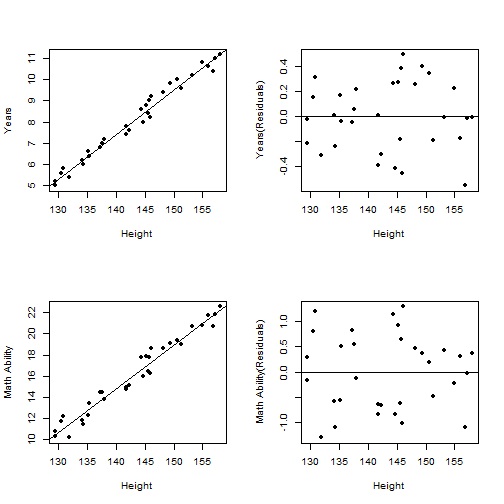
(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/8.jpg

これらの残差(身長の影響を取り除いた年齢と算数能力)の関係をプロットしてみましょう。

model6 <- lm(resid5 ~ resid4) plot(resid5 ~ resid4, xlab = "Years(Residuals)", ylab = "Math Ability(Residuals)", pch = 19) abline(model6)

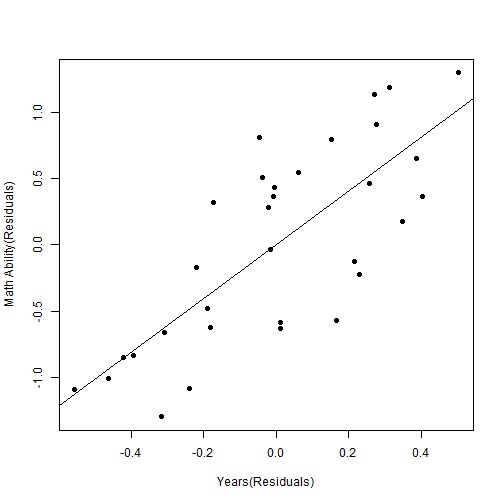
(画像が見られない方は下記URLからご覧ください）
http://px1img.getnews.jp/img/archives/2013/07/9.jpg

これらの値には、はっきりとした相関が見られます。

したがって、年齢と算数能力は、真の相関関係にあると言えます。

以上が、統計的消去の基本的な考え方です。

統計的消去を行うことで、擬似相関を見抜くことができました。

調整平方和による分散分析

この統計的消去の考え方は、分散分析にも利用されます。

上記算数能力のデータについて、まずは普通の分散分析表を出力してみましょう。

model <- lm(AMA ~ HGT + YEARS, data) anova(model)

## Analysis of Variance Table
##
## Response: AMA
## Df Sum Sq Mean Sq F value Pr(>F)
## HGT 1 413 413 1662.8 < 2e-16 *** ## YEARS 1 10 10 39.6 7.1e-07 *** ## Residuals 29 7 0 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

通常の anova() 関数では、身長(HGT)も年齢(YEARS)も両方とも有意になってしまいます。（という結果にしたかったので、わざと変数をこの順番にしています。）

これでは算数能力と身長の関係が擬似相関であることを見抜けません。

これに対して、car::Anova() 関数により、平方和のタイプを選択して実行すると、

library(car)
Anova(model, type = 2)

## Anova Table (Type II tests)
##
## Response: AMA
## Sum Sq Df F value Pr(>F)
## HGT 0.01 1 0.03 0.86
## YEARS 9.84 1 39.63 7.1e-07 ***
## Residuals 7.20 29
## —
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

年齢は有意のままですが、身長が有意ではなくなります。

これは、それぞれの変数に対して、他の変数を統計的消去した結果です。

このような分散分析を、調整平方和による分散分析といいます。（SASやSPSSは調整平方和(type III)の方がデフォルト）

「分散分析のノート」 『中西政志のウェブサイト』
http://ofmind.net/doc/anova-note#TYPES_OF_SS

まとめ

統計的消去により擬似相関を見抜くことができました。

統計的消去の原理は非常に簡単だったと思います。

しかし、擬似相関を見抜くために本当に難しいのは、今回の年齢のように原因となっている変数を見つけ出すことだと思いますので、そこらへんは頑張っていただくしかなさそうです。

以上です。

執筆： この記事はhoxo_mさんのブログ『ほくそ笑む』からご寄稿いただきました。

寄稿いただいた記事は2013年07月19日時点のものです。