「月を入力すると日を返す多項式」と中国剰余定理（tsujimotterのノートブック）

今回はtsujimotterさんのブログ『tsujimotterのノートブック』からご寄稿いただきました。

「月を入力すると日を返す多項式」と中国剰余定理（tsujimotterのノートブック）

「月を入力すると日を返す多項式」の話が、Twitterのタイムライン上で話題になりました。

「上司のおっさんに「月を入力すると日数が出るようにするにはどうすれば？」と聞かれたのでコレを教えてあげた心温まる話」『togetter』
https://togetter.com/li/1279312

どんな話題かというと、多項式 f(x) を以下のように定義したとき

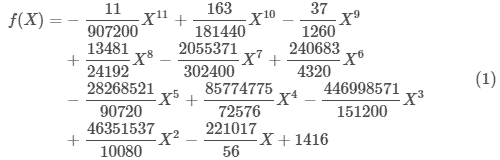
この f(X) に X=1,2,3,⋯,12 を代入すると、

　　　f(1)=31
　　　f(2)=28
　　　f(3)=31
　　　　　⋮
　　　f(12)=31

となり、月を入力すると日を返す多項式になっています！すごい！

こんな多項式をいったいどうやって求めるんだろうかと、気になったかたはいるんじゃないかと思います。

これについては 中国剰余定理 が使えるということを、Iwao KIMURA ( @iwaokimura ) さんが、以下のツイートで教えてくださいました。

月を入力すると日を返す多項式．中国の剰余定理のいい例ですね．sagemathだとコマンド一発． pic.twitter.com/F15nosE2ia

— Iwao KIMURA (@iwaokimura) 2018年10月21日

月を入力すると日を返す多項式．中国の剰余定理のいい例ですね．sagemathだとコマンド一発．

中国剰余定理は私の好きな定理の一つですが、このような応用があることはまったく知りませんでした。

とても興味深い話だったので、理屈を自分でも考えてみました。今日はそれを紹介したいと思います。

そもそも中国剰余定理とは

こんな問題を聞いたことはありませんか？

3で割ると2余り、5で割ると3余り、7で割ると2余る数は何か

答えの一つをあげると 23 です。

実際、x=23 とすると

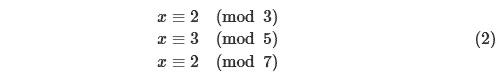
が成り立ちますね。

実は、x≡23(mod105) であれば、x は上の３つの合同式を満たします。これが上の問題のすべての解となります。なお、105=3⋅5⋅7 です。

一般に、p1,p2,⋯,pM をそれぞれ互いに素な M 個の正整数としたとき

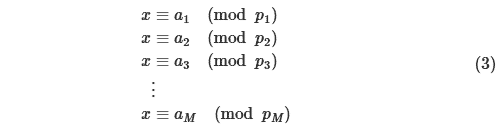
を満たす整数 x は mod p1p2⋯pM の範囲で解を持ち、その解は一意に定まります。これが 中国剰余定理 です。

「中国剰余定理」という一風変わった名前がついていますが、この名前は中国の算術書「孫子算経」に由来します。この本に「3で割ると2余り、・・・」の問題とその解法が載っていたということです。

 
中国剰余定理で一意に定まる解を「具体的に」計算する関数が sagemath にあります。
「数論」『sage』
http://doc.sagemath.org/html/ja/tutorial/tour_numtheory.html

 

実際、先ほどの問題の式 (2) を元に計算する際は

CRT([2, 3, 2], [3, 5, 7])

と打ち込んでみてください。ちゃんと 23 という答えが返ってくると思います。

“CRT” は中国剰余定理の英語名 “Chinese Remainder Theorem” の頭文字をとったものですね。

多項式環の中国剰余定理

先ほどは中国剰余定理を「整数環」という特殊な状況で考えました。実は、中国剰余定理自体は、一般の環に対しても成り立つことが知られています。

多項式環で中国剰余定理を用いると、冒頭の11次の多項式を求めることができます。どういうことか、順を追って説明しましょう。

高校のときに習ったように、多項式 f(X) が f(a)=b を満たすとき

が成り立ちます。ここで Q(X) は多項式です。式 (4) が成り立つことは、X=a を代入すればただちに確認できます。

式 (4) は次のように解釈することもできます。

多項式 f(X) を (X−a) で割った余りは b である。

このようにして多項式に「あまり」という概念が導入されます。

以上のように考えると f(1)=31 という式は、「f(X) を (X−1) で割ったあまりが 31 である」と言い換えることができます。

中国剰余定理の状況に近づいてきました。

つまり、冒頭の「月を入力すると日を返す多項式」を与える問題は
　　f(X) を (X−1) で割ったあまりが 31 である
　　f(X) を (X−2) で割ったあまりが 28 である
　　f(X) を (X−3) で割ったあまりが 31 である
　　　　　⋮
　　f(X) を (X−12) で割ったあまりが 31 である
を同時に満たす f(X) を求めよ、という問題だったというわけです。

多項式環の中国剰余定理によると、このような f(X) は存在します。

実際、sagemathを使って f(X) を計算することができます。

R. = QQ[]
f = CRT([31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31], [x-1, x-2, x-3, x-4, x-5, x-6, x-7, x-8, x-9, x-10, x-11, x-12]); f

一行目は、多項式環 R として R=Q[X] を指定しています。有理数係数の多項式環ですね。そして、多項式環の変数を x と指定しています。この辺は「へぇ、こうやって書くのか」と思っていただければ十分です。

次の行がメインです。CRT関数の１つ目の変数に

[31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]

のようにあまりの情報を12個並べています。

CRT関数の２つ目の変数には、対応する mod を並べます。

[x-1, x-2, x-3, x-4, x-5, x-6, x-7, x-8, x-9, x-10, x-11, x-12]

これらの変数を CRT([…], […]) に入れて、結果を変数 f に格納して f を出力しています。

 
これによって、求める多項式を計算することができます。実際に先のコマンドを打ち込むと、次の結果が返ってくるはずです。

-11/907200*x^11 + 163/181440*x^10 – 37/1260*x^9 + 13481/24192*x^8 – 2055371/302400*x^7 + 240683/4320*x^6 – 28268521/90720*x^5 + 85774775/72576*x^4 – 446998571/151200*x^3 + 46351537/10080*x^2 – 221017/56*x + 1416

たしかに、冒頭の多項式 (1) になっていますね！すごい！

これがちゃんと「日を返す多項式」になっていることは以下のように確認できるでしょう。

f(1)
f(2)
f(3)
f(4)
f(5)
f(6)
f(7)
f(8)
f(9)
f(10)
f(11)
f(12)

結果は次のようになるはずです。ぜひ確かめてみてください。

31
28
31
30
31
30
31
31
30
31
30
31

私の好きな中国剰余定理がこのような形で役に立つということが面白かったです！

楽しい話題をありがとうございました！

簡単ですが、今日はこの辺で。

おまけ

中国剰余定理はベルヌーイ数を計算するのにも役に立ちます！

非正則素数チェッカー #日曜数学会 from Junpei Tsuji

「非正則素数チェッカー #日曜数学会 from Junpei Tsuji」『slideshare』
https://www.slideshare.net/junpeitsuji/ss-81062660

執筆： この記事はtsujimotterさんのブログ『tsujimotterのノートブック』からご寄稿いただきました。

寄稿いただいた記事は2018年10月27日時点のものです。