数式で思いは通じるのか!?　「数学のお兄さん」に数式を使った告白法を教えてもらった

以前、数学で愛の告白ができると話題になったのをご存知ですか？ 「128√e980」の式の上部分を隠すと「I LOVE YOU」と読めるというもの。実はこれ以外にも数学で告白する方法があるそうです。

今回は「数学のお兄さん」という愛称で数学をテーマにした企画をしている横山明日希さんに数学を使ったさまざまな告白法を教えてもらいました。横山明日希さん

 

草食系男子への告白

 

横山さん：まずはアプローチが難しい草食系男子へ告白するときにぴったりの方法を紹介しますね。やっぱり草食系ですから、直接告白するよりも手紙で伝えたほうがいいでしょう。

そこで、この方程式を書いて渡してください。

 

問い：Iについて解いてね。

U-I＜2（2U-I）

 

ライター：ラブレターというよりも、普通の方程式ですね。

 

横山さん：この方程式を解くと、「I」つまり「私」のことがわかるわけです。答えを出すには、まず共通項を整理して……

 

横山さん：はい、答えは「I＜3U」になりましたね。

 

ライター：……これで完成ですか？ 普通に方程式を解いただけで、全く告白になってないですけど。

 

横山さん：よく見てください。「＜3」の部分……ハートに見えませんか？ そう、つまり「I ハートマーク U」。「I love you（U）」になってるでしょ？

 

 

ライター：本当だ！ 納得、とまではいかないけど、見えなくもない……！

 

横山さん：これくらいさりげない伝え方のほうが、草食男子にとってはいいと思います。草食系の彼が自力で方程式を解いて相手の気持ちに気づくことができたら、彼自身もちょっとだけ積極性が出て成長につながると思います。これなら付き合ってからもお互いを高めあえるいい関係になれそうですよね。

 

ライター：（こんな感じの告白の仕方がこの先も続くかと思うと不安……）

 

ロマンチスト女子への告白

 

横山さん：次のシチュエーションは、「ロマンチストな人への告白法」。やっぱり、ムードを大事にする女子にはちょっと手の込んだ告白のほうが喜ばれると思います。この場合も、さっきと同じように次の問題を出してあげましょう。

 

 

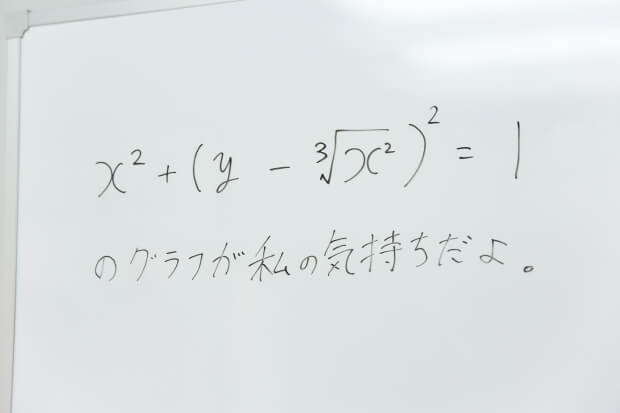
ライター：x２＋（y－……、すみません。ちょっと数学が苦手なので早くも挫折しそうです。

 

横山さん：丁寧に解いてあげれば絶対にわかりますから大丈夫です。まず、xが0のときに、yは1と-1ですね……って聞いてますか？

 

ライター：いや、ちょっと頭がすでにパンクしてしまってもう無理かもしれません。

 

横山さん：……そんな人でも一発で解ける、おすすめの秘策があります。

 

 

横山さん：グラフ描画ソフトやアプリに頼れば一発で答えが出るので、この数式をそのままソフトに入力してください。

 

ライター：そんなやり方はアリなんですか!?

 

横山さん：ではもう一度自力で解いていきましょうか。xが0のときにyは……

 

ライター：やっぱりソフトにこの式を入れてみましょうか！

 

 

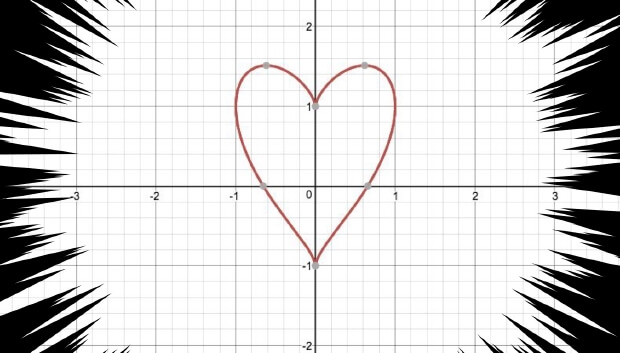
横山さん：はい、ではできたグラフがこちらです。

 

ライター：ハートになってる！ すごい！

 

横山さん：どうですか？ これならロマンチストなタイプに情熱が伝わりそうでしょう。

 

ライター：そうですね。途中でソフトを使うというロマンのかけらもない手法を使った以外はすごくロマンチックだと思います！

 

卒業式での告白

 

横山さん：これからの卒業シーズンに最適な告白も、数学の考え方を使ってできちゃいます。卒業式での定番の告白のセリフというと何が思いつきますか？

 

ライター：「ずっと前から好きでした」とかですかね。

 

横山さん：そうですよね。ただ、このセリフってよく考えるとおかしいですよね。だって、「好き“でした”」と過去形で言っているんですよ。告白をするということは、きっとまだ好きなんですよね。

証明手法である「数学的帰納法」を用いれば、もっと将来を含めた告白をすることができます。

 

 

横山さん：「ずっと前から好きでした。昨日も好きだったし今日も好きです。一日経っても好きだということは、数学的帰納法が成り立つので明日も明後日もずっとずっと好きなんです！ 付き合ってください」

 

ライター：なるほど！ 数学上でも相手を永遠に好きなことが成り立っているなんてなんだかロマンチックですね。

 

横山さん：いや、実は、厳密にいうと数学的帰納法が成り立たないパターンなんです。今日も明日も好きだからという証明はできても、明後日には変わっている可能性はまだ考えられますから。

まぁそこに気づくなら、数学が好きな人だから、数学を使って告白をしてくれた相手に対して好意的に思うはずなので……結果的にうまくいくと思います！

 

ライター：（そうなのかな……）

 

あまり共通点がない人への告白

 

横山さん：最後は、恋愛で一番大事なことなのでよく聞いてほしいです。

 

ライター：難しい数式を使わなければ大丈夫です。

 

横山さん：大丈夫です。たとえば、好きな人とは趣味がバラバラだったり、価値観が違う場合もありますよね。そんな共通点が少ない人にも、納得してもらえる言い方を数学の「集合」を使って告白することができます。

 

ライター：どんな内容かは忘れましたが、「集合」って習った記憶にあります。めちゃめちゃなつかしいですね。

 

横山さん：そしたら、だいたい覚えていますかね。2つの集合AとBに対して,どちらの集合にも属する要素全体の集合のことを「共通集合」もしくは「積集合」といい、どちらか一方の集合に属する要素全体の集合のことを「和集合」といいますよね。たとえば、Aを2の倍数、Bを3の倍数とするならば、「共通集合」は「6、12、18……」、「和集合」は「2、3、4、6、8……」となり……

 

ライター：やっぱりちょっと難しいので早めに告白のセリフをお願いします。

 

横山さん：まぁ、以上の考え方から、こんなふうに言ってあげるといいんじゃないかと思います。

 

 

横山さん：「お互いの共通集合は少ないかもしれないけど、和集合で考えると付き合えばお互い知らないことをたくさん知り合える関係になれるんだ。ぜひ、和集合的な関係でお付き合いしませんか」

 

ライター：なるほど。共通の話題があるほうが相手との距離も近づくし、つい自分と似ている人を選んでしまいがちだけど、自分と違うタイプのほうが世界も広がりますよね。意見がぶつかったときでも、和集合だということを頭に入れておけば恋愛もうまくいきそうです。

最後の最後にして、めちゃめちゃ深い。数学よりも大事なことを教えてもらった気がします。ありがとうございました！

 

まとめ

告白したい相手がかなりの数学マニアでない限り、どう考えても数学を使って告白しようと思う人なんていないかもしれません。ただ、人の気持ちは目に見えないからこそ、なかなかうまく伝わらないこともあります。そんなときに数学を使ってうまく思いを伝えてあげれば、意外と気持ちが届くのかもしれません。

春は出会いの季節でもありますから、ぜひ参考にしてみてはいかがでしょうか。ただ、うまくいかなくても決して責任は取れません！ ごめんなさい！ みなさん、素敵な春をお過ごしください！

  取材協力：横山明日希

数学の楽しさを伝える「数学のお兄さん」として活動中。数学×お笑い、数学×恋愛、数学×俳句など、「数学と何かを組み合わせる」という今までになかった切り口を中心に講演、執筆、授業、イベント企画などを行っている。

 

文：成瀬瑛理子 撮影：猿田祐樹

関連記事リンク（外部サイト）

【卒業式あるある ～高校編～】卒アル黒歴史は鉄板ネタ！？
【Youは母国でどんなバイトしてた？Vol.2】　英会話講師にも聞いてみた！
「眠気を撃退！ 早朝バイトの朝にすること」【神出鬼没！バイトセルフケアマン】第8回